
Текущий год связан с двумя «маленькими» юбилеями –
180-летием выдающегося русского ученого и педагога
Сергея Александровича Рачинского (1833-1902) и
145-летием замечательного русского художника,
Академика живописи Николая Петровича Богданова-Бельского (1868-1945).
Между этими двумя событиями есть прямая связь.
Обнаружить ее можно на известной картине Н.П. Богданова-Бельского «Устный счет. В народной школе С.А. Рачинского», написанной в 1895-м году
и находящейся в Государственной Третьяковской Галерее.
Учитель, давший деревенским ребятам «трудную задачу», это и есть С.А. Рачинский, изображенный художником с фотографической точностью.
Представитель старинного дворянского рода, профессор, получивший в тридцать три
года кафедру естественных наук в Московском университете, он, через два года, неожиданно оставляет службу («Чин следовал ему – он службу вдруг оставил.
В деревне книжки стал читать»…)
В отличие от персонажаА.С. Грибоедова, Сергей Александрович избрал другой, более активный и действенный способ «хождения в народ». Он не просто сам «читал книжки»,
а делал все возможное, чтобы их читали крестьянские дети – надежда и будущее России.
В своем родовом имении – селе Татево Бельского уезда Смоленской губернии,
Сергей Александрович, на свои средства, строит сельскую школу. Всего же, в других селах Смоленской губернии, он построит свыше 20 подобных школ, 4 из которых будет содержать полностью. Свой богатейший педагогический опыт он обобщит в книге «Сельская школа», по выходе которой будет избран членом-корреспондентом
Академии Наук по отделению русской словесности.
Он станет всероссийски-известным человеком, получит личную благодарность от Государя Императора Николая II, но главной заботой педагога останутся его ученики.
Многих из них он «выведет в люди», оказывая ребятам материальную поддержку, ходатайствуя об их принятии в те или иные учебные заведения.
Одним из таких учеников окажется способный юный рисовальщик Коля Богданов. «Внебрачный», «Богом данный» сын батрачки, прибавивший в будущем к своей
фамилии название родного уезда.
Посмотрим на картину еще раз.
Обратим внимание на мальчика на переднем плане с выразительными, совсем не детскими глазами и сравним его с автопортретом Н.П. Богданова-Бельского (1915), находящимся в Луганском областном художественном музее (Украина).
Некоторые специалисты и многие любители живописи полагают, что в образе этого мальчика художник запечатлел самого себя…
Картины Н.П. Богданова-Бельского разбросаны по всему миру.

Вернемся, однако, к «Устному счету». Уж очень он притягателен !
На доске написано условие задачи - определить значение дроби:
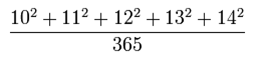
Когда-то, в году примерно 1962-м, наша «математичка», Любовь Иосифовна Драбкина, дала эту задачу и нам,
7-классникам.
Быстро посчитать в уме я не мог. Я прикинул, ответ должен выражаться целым числом. Иначе - это уже не «устный счет»! Этим числом не могла быть единица – даже если бы в числителе стояли одинаковые 5 сотен, ответ получался явно больше. С другой стороны, и до числа «3»
он явно де дотягивал.
– Два!!! – выпалил я, на секунду опередив моего друга, Леню Струкова,
лучшего математика нашей школы.
– Да, действительно два, – подтвердил Леня.
– Как Вы считали? – спросила Любовь Иосифовна.
– Я никак не считал. Интуиция – ответил я под хохот всего класса.
– Если не считал – ответ не считается – «скаламбурила» Любовь Иосифовна.
Леня, а ты тоже не считал?
– Нет, почему же, степенно ответил Леня. Надо было сложить 121, 144, 169 и 196.
Я попарно сложил числа первое и третье, второе и четвертое. Так удобнее.
Получилось 290+340. Общая сумма, включая первую сотню – 730.
Делим на 365 – получаем 2.
– Молодец! Но на будущее запомните – в ряду двузначных чисел – у первых пяти его представителей – есть удивительное свойство. Сумма квадратов первых трех чисел ряда (10, 11 и 12) равна сумме квадратов следующих двух (13 и 14). И равняется эта сумма 365. Легко запомнить! Столько дней в году. Если год не високосный. Зная это свойство, ответ можно получить за секунду. Без всякой интуиции…
…Прошли годы. В центральном переходе, под перекрестком Энгельса (сейчас – Большая Садовая) – Ворошиловский сделали целую панораму об основных этапах жизненного пути советского человека – родильный дом – детский сад - школа, выпускной бал…
На одной из «школьных» картин можно было увидеть знакомую сцену – решение задачи. Назовем ее так: «Задачи Рачинского»
Проходили годы, проходили люди. Веселые и грустные, молодые и не очень.
Кто-то вспоминал свою школу, кто-то при этом «шевелил мозгами»
Сейчас «ростовское чудо» «временно недоступно».
